Kalman Filters
One of the projects in Learning in Robotics (ESE650) was using an Unscented Kalman Filter to estimate the orientation of an object using gyroscope and accelerometer data. It was based on this paper by Edgar Kraft. The algorithm maintains a state estimate with an angular velocity vector and the current orientation as a quaternion. It then estimates what the measurements should be and compares this to the actual measurements to generate an error term that is used to correct the state. At the same time, it maintains a covariance matrix with the certainties in order to weight the relative importance of the state estimate and the estimate from the measurements.
Implementing it didn't take too long, but it did take a little while to figure out how to do some of the quaternion operations, especially averaging and adding an error vector. I also ran into several problems, such as an integer division issue that only appeared on the grading server, because I was using Python 3. Eventually fixed a few issues and tuned it until it was working well, as shown below. Unfortunately, I still had a bug that caused the yaw angle to tend towards 0, even though there's no way for the filter to determine the yaw angle. By the time I realized that was an issue, I had run out of time to finish debugging.
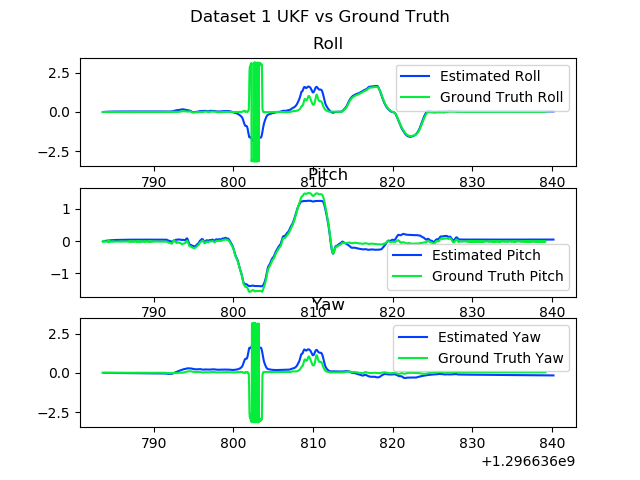
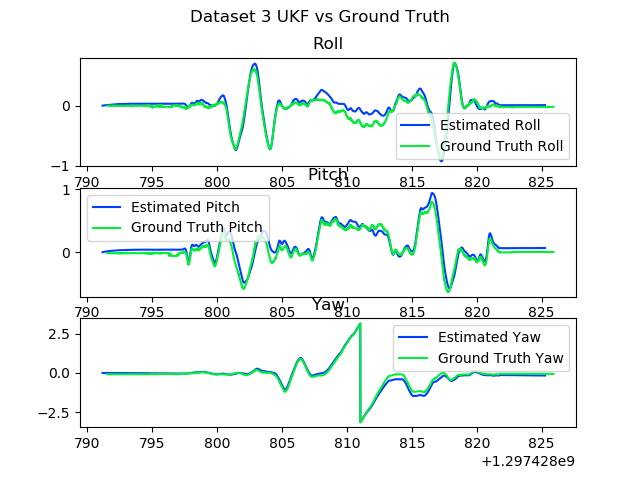
In the next project, we're using an Extended Kalman Filter to map the locations of trees based on lidar measurements, GPS positions and a motion model.