Quadcopter Control

In Advanced Robotics (MEAM620), I created a nonlinear quadcopter controller, implemented A* and designed a trajectory generator. The controller has two parts, the position controller and the attitude controller, that work together to follow a given trajectory. The position controller calculates the desired force based on the trajectory's acceleration and the position and velocity error. A thrust is commanded that is equal to the magnitude of this force along the vertical axis of the quadcopter. At the same time, the attitude controller calculates the rotation between the desired angle and the actual angle and uses PD control to match the desired attitude.

The maps were discretized into a 3D grid for A* to search through. Implementing A* in MATLAB was inconvenient because of the indexing tricks that I used to make it run fast enough. I also wrote a priority queue to improve the efficiency further, but found that it was actually 30% slower, because MATLAB is so slow at executing anything written in MATLAB. Another variant I experimented allowed diagonal moves, but I found this actually performed slightly worse with the way my trajectory generator optimized the path.

I experimented with different methods of trajectory generation, but found that simple lines with linear acceleration were sufficiently fast. Quadcopters are a fourth order system and therefore this introduced discontinuities, but my controller is stable enough to deal with them. To keep the paths short, the trajectory generator removes vertices whenever the line between won't hit an obstacle. It performs two passes and could be improved to find slightly shorter paths, but this was enough to find fast enough paths for all the tests.

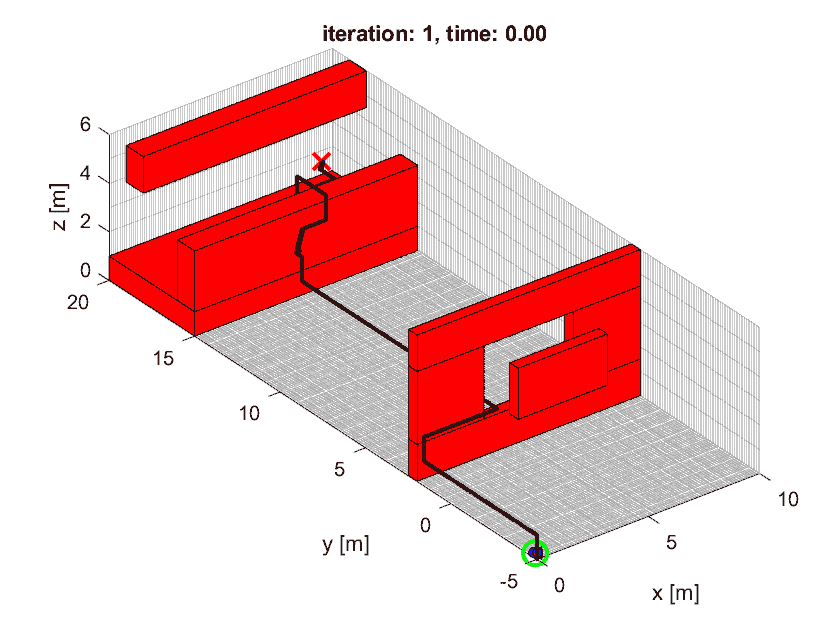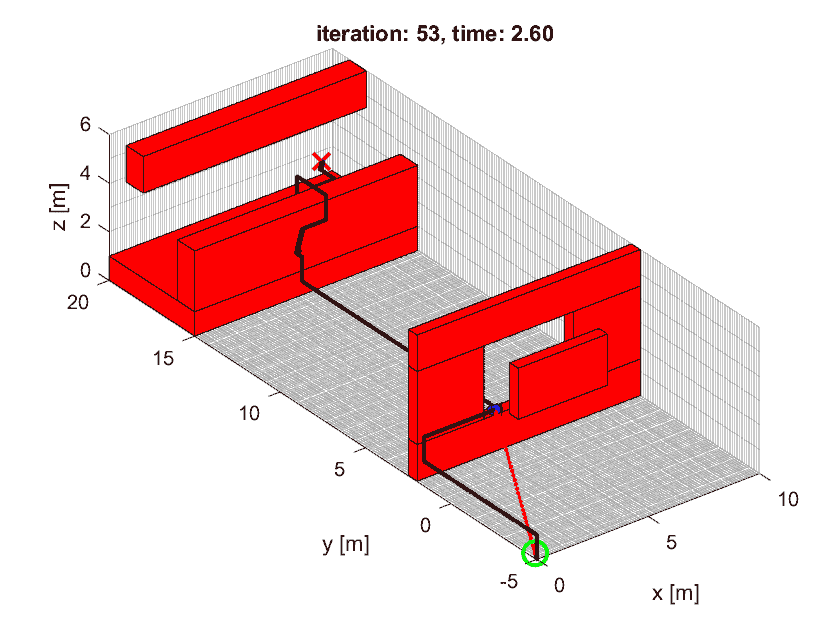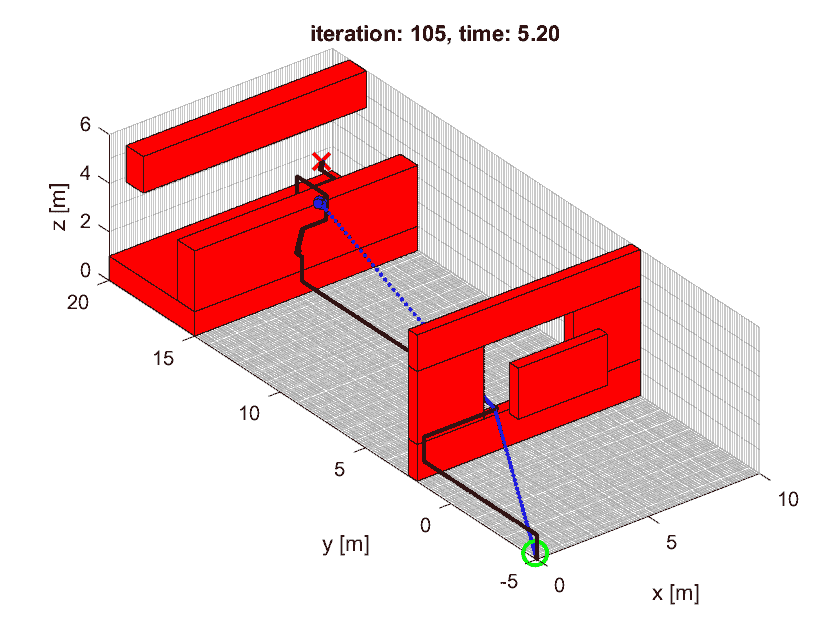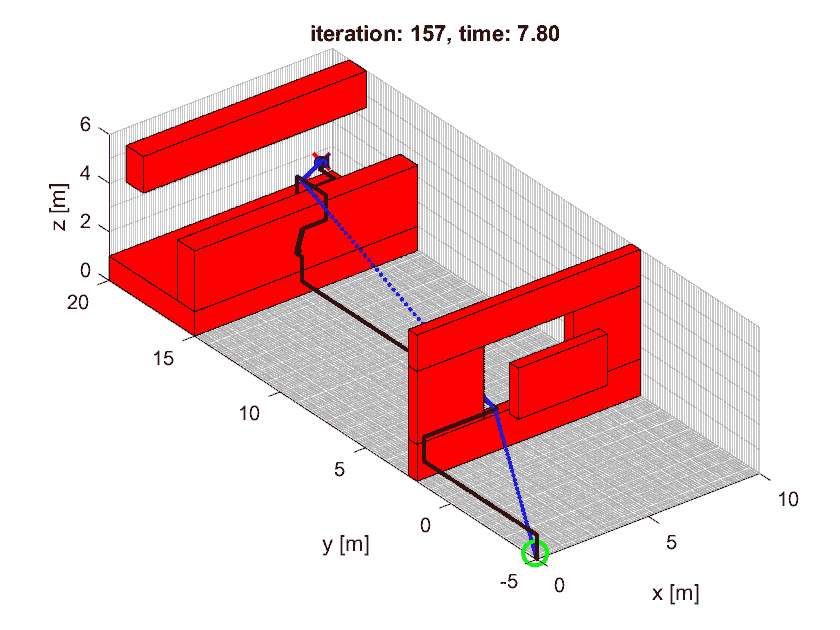
Once this worked well in the provided simulation, we went to a lab in groups to see how well the code would work in the real world. My controller was stable once we lowered the gains a bit. We also tested my trajectory generator and it successfully navigated a maze quickly while avoiding the obstacles.

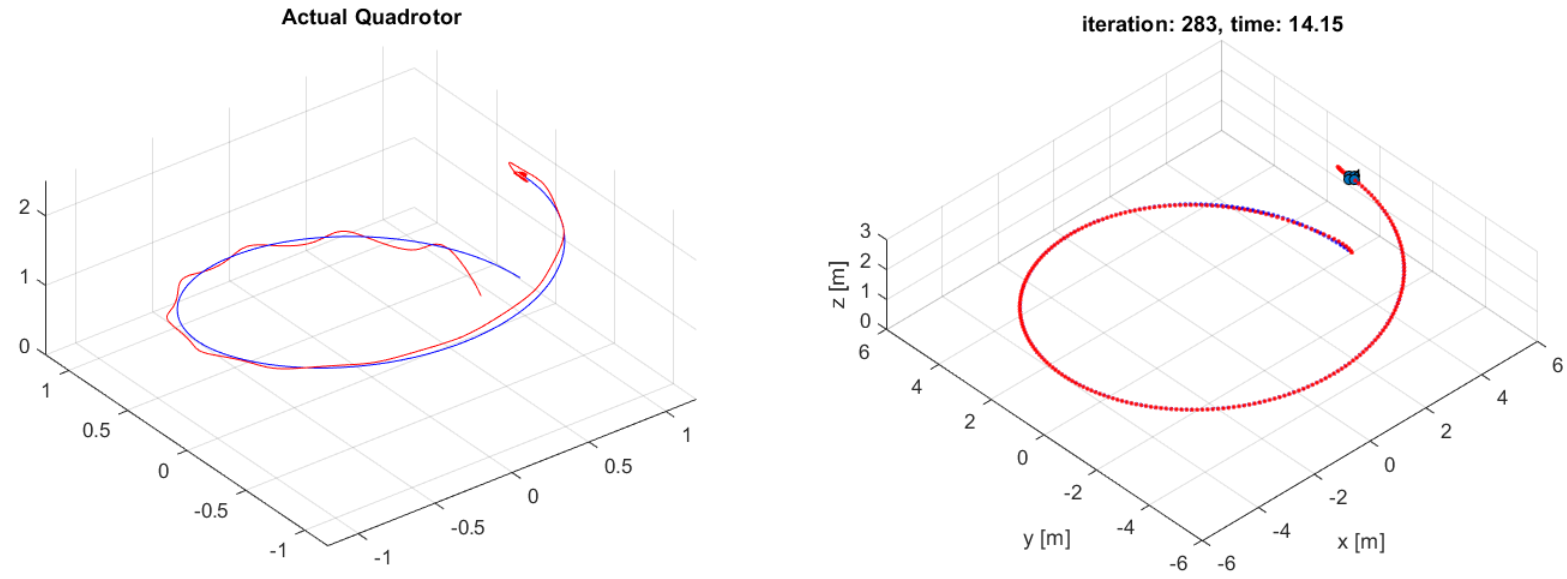
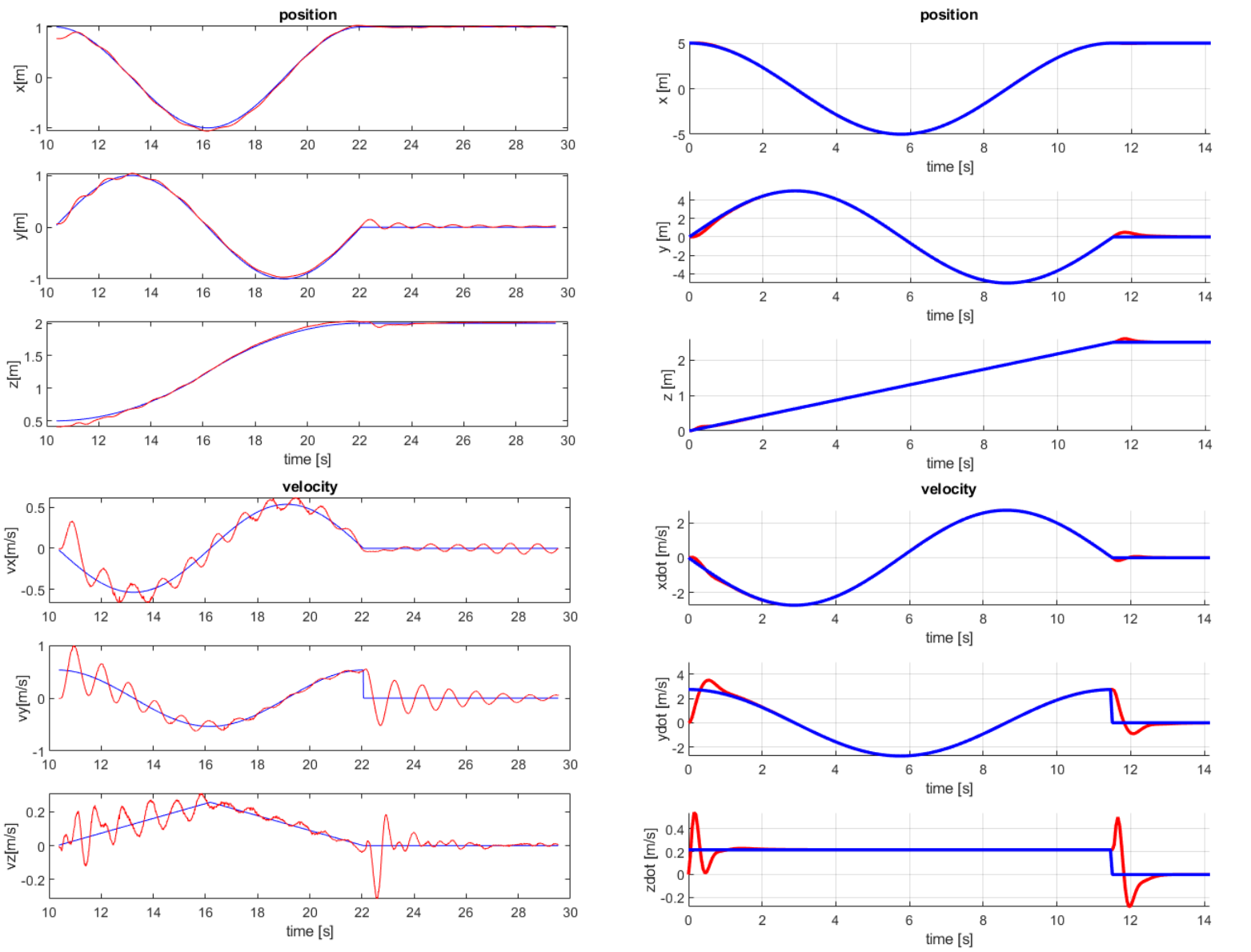
In addition to going through a maze, we compared the results to a helix trajectory that was similar to one in simulation. We didn't have much time to tune the controller and real world disturbances and error caused the quadcopter to perform worse. Nevertheless, it tracked the trajectory well.